Skip to main content

10: 平滑图像

学习模糊/平滑图像，消除噪点。图片等可到文末引用处下载。

目标​

  • 模糊/平滑图片来消除图片噪声
  • OpenCV 函数：cv2.blur(), cv2.GaussianBlur(), cv2.medianBlur(), cv2.bilateralFilter()

教程​

滤波与模糊​

推荐大家先阅读：番外篇：卷积基础(图片边框)，有助于理解卷积和滤波的概念。

关于滤波和模糊，很多人分不清，我来给大家理理（虽说如此，我后面也会混着用，,ԾㅂԾ,,）：

  • 它们都属于卷积，不同滤波方法之间只是卷积核不同（对线性滤波而言）
  • 低通滤波器是模糊，高通滤波器是锐化

低通滤波器就是允许低频信号通过，在图像中边缘和噪点都相当于高频部分，所以低通滤波器用于去除噪点、平滑和模糊图像。高通滤波器则反之，用来增强图像边缘，进行锐化处理。

常见噪声有椒盐噪声和高斯噪声，椒盐噪声可以理解为斑点，随机出现在图像中的黑点或白点；高斯噪声可以理解为拍摄图片时由于光照等原因造成的噪声。

均值滤波​

均值滤波是一种最简单的滤波处理，它取的是卷积核区域内元素的均值，用cv2.blur()实现，如 3×3 的卷积核：

kernel=19[111111111]kernel = \frac{1}{9}\left[ \begin{matrix} 1 & 1 & 1 \newline 1 & 1 & 1 \newline 1 & 1 & 1 \end{matrix} \right]
img = cv2.imread('lena.jpg')
blur = cv2.blur(img, (3, 3))  # 均值模糊

所有的滤波函数都有一个可选参数 borderType，这个参数就是番外篇：卷积基础(图片边框)中所说的边框填充方式。

方框滤波​

方框滤波跟均值滤波很像，如 3×3 的滤波核如下：

k=a[111111111]k = a\left[ \begin{matrix} 1 & 1 & 1 \newline 1 & 1 & 1 \newline 1 & 1 & 1 \end{matrix} \right]

用cv2.boxFilter()函数实现，当可选参数 normalize 为 True 的时候，方框滤波就是均值滤波，上式中的 a 就等于 1/9；normalize 为 False 的时候，a=1，相当于求区域内的像素和。

# 前面的均值滤波也可以用方框滤波实现：normalize=True
blur = cv2.boxFilter(img, -1, (3, 3), normalize=True)

高斯滤波​

前面两种滤波方式，卷积核内的每个值都一样，也就是说图像区域中每个像素的权重也就一样。高斯滤波的卷积核权重并不相同：中间像素点权重最高，越远离中心的像素权重越小，来，数学时间( ╯□╰ )，还记得标准正态分布的曲线吗？

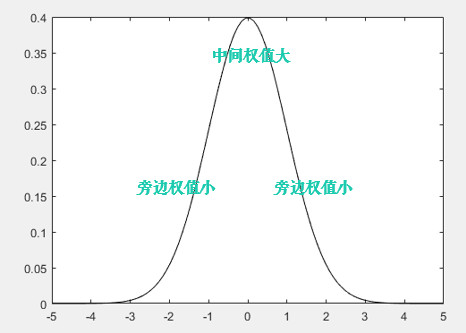
显然这种处理元素间权值的方式更加合理一些。图像是 2 维的，所以我们需要使用2 维的高斯函数，比如 OpenCV 中默认的 3×3 的高斯卷积核（具体原理和卷积核生成方式请参考文末的番外小篇）：

k=[0.06250.1250.06250.1250.250.1250.06250.1250.0625]k = \left[ \begin{matrix} 0.0625 & 0.125 & 0.0625 \newline 0.125 & 0.25 & 0.125 \newline 0.0625 & 0.125 & 0.0625 \end{matrix} \right]

OpenCV 中对应函数为cv2.GaussianBlur(src,ksize,sigmaX)：

img = cv2.imread('gaussian_noise.bmp')
# 均值滤波 vs 高斯滤波
blur = cv2.blur(img, (5, 5))  # 均值滤波
gaussian = cv2.GaussianBlur(img, (5, 5), 1)  # 高斯滤波

参数 3 σx 值越大，模糊效果越明显。高斯滤波相比均值滤波效率要慢，但可以有效消除高斯噪声，能保留更多的图像细节，所以经常被称为最有用的滤波器。均值滤波与高斯滤波的对比结果如下（均值滤波丢失的细节更多）：

中值滤波​

中值又叫中位数，是所有数排序后取中间的值。中值滤波就是用区域内的中值来代替本像素值，所以那种孤立的斑点，如 0 或 255 很容易消除掉，适用于去除椒盐噪声和斑点噪声。中值是一种非线性操作，效率相比前面几种线性滤波要慢。

比如下面这张斑点噪声图，用中值滤波显然更好：

img = cv2.imread('salt_noise.bmp', 0)
# 均值滤波 vs 中值滤波
blur = cv2.blur(img, (5, 5))  # 均值滤波
median = cv2.medianBlur(img, 5)  # 中值滤波

双边滤波​

模糊操作基本都会损失掉图像细节信息，尤其前面介绍的线性滤波器，图像的边缘信息很难保留下来。然而，边缘（edge）信息是图像中很重要的一个特征，所以这才有了双边滤波。用cv2.bilateralFilter()函数实现：

img = cv2.imread('lena.jpg')
# 双边滤波 vs 高斯滤波
gau = cv2.GaussianBlur(img, (5, 5), 0)  # 高斯滤波
blur = cv2.bilateralFilter(img, 9, 75, 75)  # 双边滤波

可以看到，双边滤波明显保留了更多边缘信息。

番外小篇：高斯滤波卷积核​

要解释高斯滤波卷积核是如何生成的，需要先复习下概率论的知识（What？？又是数学( ╯□╰ )）

一维的高斯函数/正态分布$ X\sim N(\mu, \sigma^2) $：

G(x)=12πσexp(−(x−μ)22σ2)G(x)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})

当$ \mu=0, \sigma^2=1 时，称为标准正态分布时，称为标准正态分布 X\sim N(0, 1) $：

G(x)=12πexp(−x22)G(x)=\frac{1}{\sqrt{2\pi}}exp(-\frac{x^2}{2})

二维 X/Y 相互独立的高斯函数：

G(x,y)=12πσxσyexp(−(x−μx)2+(y−μy)22σxσy)=G(x)G(y)G(x,y)=\frac{1}{2\pi\sigma_x\sigma_y}exp(-\frac{(x-\mu_x)^2+(y-\mu_y)^2}{2\sigma_x\sigma_y})=G(x)G(y)

由上可知，二维高斯函数具有可分离性，所以 OpenCV 分两步计算二维高斯卷积，先水平再垂直，每个方向上都是一维的卷积。OpenCV 中这个一维卷积的计算公式类似于上面的一维高斯函数：

G(i)=α∗exp(−(i−ksize−12)22σ2)G(i)=\alpha *exp(-\frac{(i-\frac{ksize-1}{2})^2}{2\sigma^2})

其中 i=0…ksize-1，α 是一个常数，也称为缩放因子，它使得\(\sum{G(i)}=1\)

比如我们可以用cv2.getGaussianKernel(ksize,sigma)来生成一维卷积核：

  • sigma<=0 时，sigma=0.3*((ksize-1)*0.5 - 1) + 0.8
  • sigma>0 时，sigma=sigma
print(cv2.getGaussianKernel(3, 0))
# 结果：[[0.25][0.5][0.25]]

生成之后，先进行三次的水平卷积：

I×[0.250.50.250.250.50.250.250.50.25]I×\left[ \begin{matrix} 0.25 & 0.5 & 0.25 \newline 0.25 & 0.5 & 0.25 \newline 0.25 & 0.5 & 0.25 \end{matrix} \right]

然后再进行垂直的三次卷积：

I×[0.250.50.250.250.50.250.250.50.25]×[0.250.250.250.50.50.50.250.250.25]=I×[0.06250.1250.06250.1250.250.1250.06250.1250.0625]I×\left[ \begin{matrix} 0.25 & 0.5 & 0.25 \newline 0.25 & 0.5 & 0.25 \newline 0.25 & 0.5 & 0.25 \end{matrix} \right]×\left[ \begin{matrix} 0.25 & 0.25 & 0.25 \newline 0.5 & 0.5 & 0.5 \newline 0.25 & 0.25 & 0.25 \end{matrix} \right] =I×\left[ \begin{matrix} 0.0625 & 0.125 & 0.0625 \newline 0.125 & 0.25 & 0.125 \newline 0.0625 & 0.125 & 0.0625 \end{matrix} \right]

这就是 OpenCV 中高斯卷积核的生成方式。其实，OpenCV 源码中对小于 7×7 的核是直接计算好放在数组里面的，这样计算速度会快一点，感兴趣的可以看下源码：getGaussianKernel()

上面矩阵也可以写成：

116[121242121]\frac{1}{16}\left[ \begin{matrix} 1& 2 & 1 \newline 2 & 4 & 2 \newline 1 & 2 & 1 \end{matrix} \right]

小结​

  • 在不知道用什么滤波器好的时候，优先高斯滤波cv2.GaussianBlur()，然后均值滤波cv2.blur()。
  • 斑点和椒盐噪声优先使用中值滤波cv2.medianBlur()。
  • 要去除噪点的同时尽可能保留更多的边缘信息，使用双边滤波cv2.bilateralFilter()。
  • 线性滤波方式：均值滤波、方框滤波、高斯滤波（速度相对快）。
  • 非线性滤波方式：中值滤波、双边滤波（速度相对慢）。

接口文档​

引用​