Skip to main content

番外篇：Otsu 阈值法

大部分图像处理任务都需要先进行二值化操作，阈值的选取很关键，Otsu 阈值法会自动计算阈值。

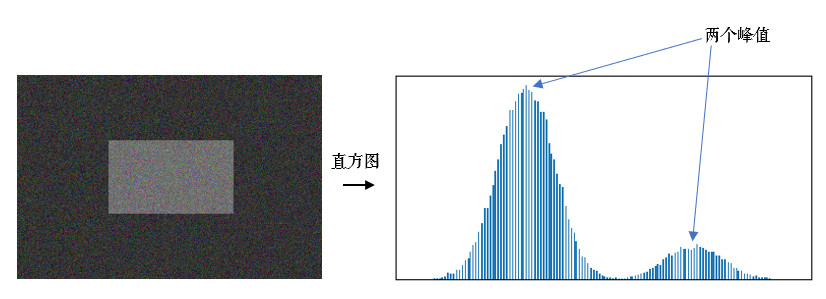
Otsu 阈值法（日本人大津展之提出的，也可称大津算法）非常适用于双峰图片，啥意思呢？

Otsu N. A threshold selection method from gray-level histograms[J]. IEEE transactions on systems, man, and cybernetics, 1979, 9(1): 62-66.

什么是双峰图片？​

双峰图片就是指图片的灰度直方图上有两个峰值，直方图就是每个值（0~255）的像素点个数统计，后面会详细介绍。

Otsu 算法假设这副图片由前景色和背景色组成，通过统计学方法（最大类间方差）选取一个阈值，将前景和背景尽可能分开，我们先来看下代码，然后详细说明下算法原理。

代码示例​

下面这段代码对比了使用固定阈值和 Otsu 阈值后的不同结果：

另外，对含噪点的图像，先进行滤波操作效果会更好。

import cv2
from matplotlib import pyplot as plt

img = cv2.imread('noisy.jpg', 0)

# 固定阈值法
ret1, th1 = cv2.threshold(img, 100, 255, cv2.THRESH_BINARY)

# Otsu 阈值法
ret2, th2 = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)

# 先进行高斯滤波，再使用 Otsu 阈值法
blur = cv2.GaussianBlur(img, (5, 5), 0)
ret3, th3 = cv2.threshold(blur, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)

下面我们用 Matplotlib 把原图、直方图和阈值图都显示出来：

images = [img, 0, th1, img, 0, th2, blur, 0, th3]
titles = ['Original', 'Histogram', 'Global(v=100)',
          'Original', 'Histogram', "Otsu's",
          'Gaussian filtered Image', 'Histogram', "Otsu's"]

for i in range(3):
    # 绘制原图
    plt.subplot(3, 3, i * 3 + 1)
    plt.imshow(images[i * 3], 'gray')
    plt.title(titles[i * 3], fontsize=8)
    plt.xticks([]), plt.yticks([])

    # 绘制直方图 plt.hist，ravel 函数将数组降成一维
    plt.subplot(3, 3, i * 3 + 2)
    plt.hist(images[i * 3].ravel(), 256)
    plt.title(titles[i * 3 + 1], fontsize=8)
    plt.xticks([]), plt.yticks([])

    # 绘制阈值图
    plt.subplot(3, 3, i * 3 + 3)
    plt.imshow(images[i * 3 + 2], 'gray')
    plt.title(titles[i * 3 + 2], fontsize=8)
    plt.xticks([]), plt.yticks([])
plt.show()

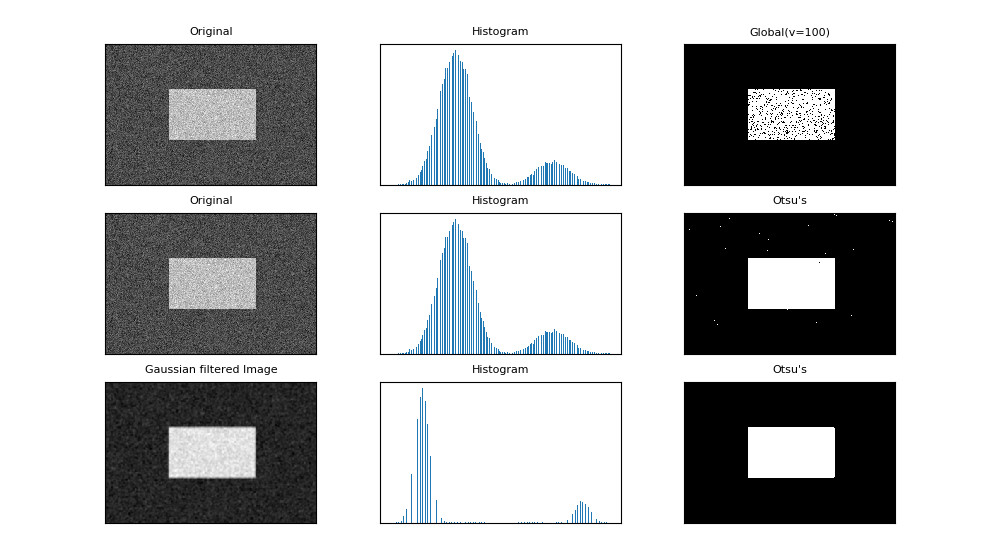
固定阈值 vs Otsu阈值

可以看到，Otsu 阈值明显优于固定阈值，省去了不断尝试阈值判断效果好坏的过程。其中，绘制直方图时，使用了 numpy 中的ravel()函数，它会将原矩阵压缩成一维数组，便于画直方图。

Otsu 算法详解​

Otsu 阈值法将整幅图分为前景（目标）和背景，以下是一些符号规定：

  • $ T $：分割阈值
  • $ N_0 $：前景像素点数
  • $ N_1 $：背景像素点数
  • $ \omega_0 $：前景的像素点数占整幅图像的比例
  • $ \omega_1 $：背景的像素点数占整幅图像的比例
  • $ \mu_0 $：前景的平均像素值
  • $ \mu_1 $：背景的平均像素值
  • $ \mu $：整幅图的平均像素值
  • $ rows\times cols $：图像的行数和列数

结合下图会更容易理解一些，有一副大小为 4×4 的图片，假设阈值 T 为 1，那么：

其实很好理解，$ N_0+N_1 $就是总的像素点个数，也就是行数乘列数：

N0+N1=rows×colsN_0+N_1=rows\times cols

$ \omega_0 和和 \omega_1 $是前/背景所占的比例，也就是：

ω0=N0rows×cols\omega_0=\frac{N_0}{rows\times cols}
ω1=N1rows×cols\omega_1=\frac{N_1}{rows\times cols}
ω0+ω1=1(1)\omega_0+\omega_1=1 \tag{1}

整幅图的平均像素值就是：

μ=ω0×μ0+ω1×μ1(2)\mu=\omega_0\times \mu_0+\omega_1\times \mu_1 \tag{2}

此时，我们定义一个前景$ \mu_0 与背景与背景 \mu_1 的方差的方差 g $：

g=ω0(μ0−μ)2+ω1(μ1−μ)2(3)g=\omega_0(\mu_0-\mu)^2+\omega_1(\mu_1-\mu)^2 \tag{3}

将前述的 1/2/3 公式整合在一起，便是：

g=ω0ω1(μ0−μ1)2g=\omega_0\omega_1(\mu_0-\mu_1)^2

$ g 就是前景与背景两类之间的方差，这个值越大，说明前景和背景的差别也就越大，效果越好。Otsu算法便是遍历阈值T，使得就是前景与背景两类之间的方差，这个值越大，说明前景和背景的差别也就越大，效果越好。Otsu 算法便是遍历阈值 T，使得 g $最大，所以又称为最大类间方差法。基本上双峰图片的阈值 T 在两峰之间的谷底。

接口文档​

引用​